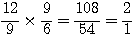|

S'abonner au bulletin
MANUEL D'HARMONIQUE
DE
NICOMAQUE - DE GÉRASE
PITHAGORICIEN
_______________
Ce texte est la traduction du grec de Charles Émile Ruelle et publié dans l'«annuaire de l'Association pour l'encouragement des Études grecques en France» (1880), Paris, Baur 1881. Cette traduction est aujourd'hui encore pertinente. Nous avons reporté les notes de bas de page en marge en leur avons donné une numérotation continue. Nicomaque de Gérase est un mathématicien grec néo-pythagoricien
né en Palestine à Gerasa (Jordanie), ayant vécu vers les années 150-200
[Lire les fragments relatifs à l'Harmonique]
|
SOMMAIRE DES CHAPITRES (1)
1. Ce manuel est un commentaire sur les éléments harmoniques.
2. Des deux espèces de voix, la voix discontinue et la voix continue ; de leurs régions.
3. Parmi les choses sensibles, c'est la musique planétaire qui est considérée en premier lieu, puis, à l'imitation de cette -musique, celle qui a cours chez nous autres hommes.
4. La science des sons est réglée par les nombres.
5. Pythagore, en ajoutant une huitième corde à. la lyre heptacorde, a constitué l'harmonie de diapason (octave).
6. Comment furent découverts les rapports numériques des sons.
7. La division du diapason (octave) . dans le genre diatonique.
8. Explication des points relatifs à l'harmonique, contenus dans le
Timée.
9. Témoignages de Philolaüs.
10. Sur l'accord des sons suivant les rapports numériques.
11. Sur le disdiapason (double octave), suivant le genre diatonique.
12. Progression et division des sons dans les trois genres (2).
|
Page 1 du texte de Meybaum
(1) Le texte correspondant à ces rubriques est ce qu'on nomme d'ordinaire le livre Ier du
Manuel d'harmonique. (Voir l'Avertissement, p. 2.) On remarquera, que le prétendu livre II dont nous faisons un recueil d'extraits, n'a pas donné lieu à cette division par chapitres.
Mb. 2
(2) A part cette table sommaire, les manuscrits connus, non plus que les éditions, ne présentent aucune division en chapitres et en paragraphes
|
|
CHAPITRE PREMIER
1. L'exposé dees intervalles et des rapports des sons dans les éléments harmoniques est par lui-même rempli de détails et difficile à renfermer dans un commentaire unique ; d'autre part, en ce qui me concerne, la vie agitée de voyageur, et de voyageur surmené, à laquelle je suis condamné, m'ôte la possibilité d'entreprendre un tel exposé dans une pleine liberté d'esprit, et d'aborder la doctrine
relative à ces questions avec toute la clarté convenable, ce qui exigerait du loisir et un raisonnement recueilli.
2. Malgré cela, je dois mettre toits mes soins, puisque, après tout, tu me le demandes, ô la meilleure, la plus digne des femmes (3), à te faire une exposition improvisée ne fût-ce que des chapitres réduits à l'énoncé du sujet, sans préparation et sans démonstration détaillée, de façon qu'embrassant ces questions d'un seul coup d'oeil, et employant comme un manuel ce court aperçu, tu
puisses te remémorer ce que l'on dit et l'on enseigne tout au long dans chaque chapitre.
3. Dès mon premier moment de loisir et quand mes voyages auront pris fin, je composerai à ton intention une introduction plus étendue, plus développée sur ces mêmes matières et pleine, comme on dit, de raisonnements bien conduits, le tout en plusieurs livres (4), et par la première occasion je t'enverrai mon travail là où j'apprendrai que vous résidez (5). Je le ferai volontiers partir, pour l'enchaînement (des
idées), de ce qui a servi de point de départ à notre doctrine, dans le temps où je t'expliquais ces matières.
|
Mb. 3
(3) Ce Manuel est adressé à une dame, probablement une pythagoricienne. Elles étaient nombreuses. Jamblique a nommé les plus célèbres, au nombre de dix-sept. (Vie de Pythagore, chap. xxxvi.)
(4) Cette particularité prouve que l'édition de ce traité, faite par Nicomaque lui-mêne, ne formait qu'un seul livre, se terminant avec le chapitre xii. Cette remarque avait d'ailleurs été faite par Meybaum.
(5) La personne à qui s'adresse Nicomaque vivait probablement en famille.
|
|
CHAPITRE II
1. La voix humaine, selon les maîtres sortis de l'école de Pythagore, serait de deux espèces se rattachant à un seul genre, et appelées spécialement, l'une continue, l'autre discontinue. Ils tiraient ces dénominations des circonstances propres à chaque espèce. L'espèce discontinue, celle qui comporte le chant et se pose toujours sur un son, qui rend toujours manifeste l'altération produite dans les parties, ils la supposaient
exempte de confusion et divisée, graduée (6) d'après les grandeurs comprises entre chaque son, formant comme un morceau, mais non un mélange des parties de la voix situées les unes entre les autres, faciles à isoler et à distinguer, et nullement corrompues dans leur ensemble (7).
5. En effet, l'espèce chantée est de nature à faire reconnaître par une oreille exercée, au sujet de tous les sons, de quelle grandeur fait partie chacun d'eux ; Car celui qui ne fait pas cet emploi de l'espèce en question, on ne dit plus qu'il chante, mais qu'il parle.
6. L autre espèce, l'espèce continue, nous la pratiquons pour converser entre nous et pour lire, sans être aucunement contraints de faire sentir les tensions des sons (8) et de les distinguer entre elles, mais en débitant le discours tout d'un trait jusqu'à l'achèvement de ce que l'on, veut dire. Si quelqu'un, en causant ou en plaidant, ou encore en faisant une lecture, vient à manifester les grandeurs comprises entre chaque son, en espaçant
la.voix et en la faisant passer d'un son à un autre, on dit qu'il ne parle plus ou qu'il ne lit plus, mais qu'il chante.
6
bis. Étant posé que la voix humainese divise en deux parties (ces Pythagoriciens), pensaient qu'il devait avoir aussi, vraisemblablement, deux régions occupées et parcourues par chacune des deux:espèces de voix; que la région de la voix continue se trouve par sa nature indéterminée quant à la grandeur, et recevant pour limites propres le moment où l'on commence à parler et celui où l'on cesse de le faire, c'est-à-dire
depuis la première limite du discours jusqu'à la dernière limite du silence, si bien que la majeure partie de cette région est à notre discrétion.
7. Quant, à la région discontinue, elle n'est plus à notre-discrétion, mais soumise à la nature et limitée elle-même par des influences diverses. En effet, au point de départ, c'est le premier son perceptible, et son terme final, le dernier son que la voix puisse émettre ; car nous commençons à apprécier et à comprendre les grandeurs des sons et leurs altérations réciproques à partir
du point où l'on voit notre oreille commencer à percevoir, tandis qu'il peut arriver que des voix. plus confuses et non encore perceptibles à notre oreille se réalisent dans la nature tout en se dérobant encore à notre sens auditif. Tout de même que, par exemple, quand il s'agit d'une pesée, certains corps ne laissent pas du tout apprécier leur pesanteur, tels que la paille, le son, etc. Mais lorsque, de nouvelles quantités de ces substances
venant à s'ajouter, on voit déjà leur poids commencer à entraîner le fléau (de la balance), alors nous disons que le pesage en est à sa première application.
8. C'est de la méme façon que, peu à peu la confusion de la voix s'élevant à des quantités plus grandes, du premier degré perceptible à l'oreille, nous faisons le commencement de la région de la voix chantée ; quant à la fin de cette région, ce n'est plus l'oreille qui la détermine, mais la voix humaine. En effet, tant qu'elle procède mélodiquement et qu'elle marche dans les conditions du
chant, nous déterminons jusque-là la dernière limite do région de cette même voix.
9. Il ne nous importe en rien de prendre, pour sujet d'explication soit notre voix, issue des artères, soit des instruments à cordes, à vent et à percussion, construits à l'imitation de notre voix. Mais passons pour le moment sur les différences qui les distinguent afin de ne pas, dès notre début, rendre les explications trop diffuses.
|
Mb. 4
(6) Δτ εστός
(7) Il s'agit d'une corruption simultanée qui, précisément, mettait fin à cette distinction des sons, condition première de la voix chantée. Cette corruption correspond, dans l'art de la peinture, à la fusion des couleurs, Φθορά τών γρωμάτων
(8) Métaphore empruntée à la tension des cordes de la lyre. Cp. Aristoxène, où le mot άσις a toujours la même signification
Mb. 5
|
|
CHAPITRE III
10. Les noms des sons doivent avoir été empruntés aux sept astres qui parcourent le ciel et roulent autour de la terre. En effet on dit (9) que tous les corps qui tournent rapidement lorsque quelque chose leur cède la place - Jouit d'une grande fluidité, produisent nécessairement 'des bruits qui diffèrent entre eux par la grandeur, pàr la vitesse du son (10) et par son lieu; c'est-à-dire en raison de leurs sons à eux-mêmes,
de leurs vitesses propres ou des milieux dans lesquels s'accomplit la révolution de chaque corps, suivant que ces milieux se trouvent plus fluides ou au contraire plus. résistants.
11. On relève clairement ces trois mêmes différences à propos des planètes qui se distinguent entre elles par la grandeur, la vitesse, le lieu, et qui perpétuellement, sans relâche, roulent en sifflant dans la vapeur éthérée.
12. C'est précisément de là qu'est venu pour chacune d'elles le nom d' άστήϕ (astre) (11), comme qui dirait « sans station » et « courant toujours » (12), d'où l'on a formé les mots θεός (Dieu), αίθήϕ (éther).
13. Maintenant, en raison du mouvement de Cronos, qui est la planète située le plus au-dessus de nous, le son le plus grave dans le diapason a été nommé ύπάτη,
hypate (13), car ϋπατου signifie le plus élevé.
14. En raison du cours de la lune, placée au rang le plus bas et le plus près de la terre, on a dit νεάτη, nète, car νέτον signifie le plus bas (14)
15. Parmi les deux astres situés de chaque côté, à l'un, celui de Zeus, au-dessous de Cronos, correspond la
parhypate ; à l'autre, celui d'Aphrodite, situé au-dessus de la Lune, la
paranète.
16. L'astre le plus central, qui est le Soleil, placé le quatrième à partir de chaque extrême, devient l'origine de la
mèse, placée à l'intervalle de la quarte de l'un et-de l'autre [son extrême], dans l'heptacorde antique, de même que le Soleil parmi les sept planètes est au quatrième rang à partir de chaque astre extrême, puisqu'il occupe le point moyen.
17. Parmi les deux astres situés de chaque côté du soleil, à l'un, Arès, à qui échut la sphère placée entre Zeus et le Soleil, correspond l'
hypermèse appelée aussi
lichanos ; et à l'autre, Hermès, occupant le milieu entre Aphrodite et le Soleil, la
paramèse.
18. Nous te confirmerons ces notions avec une plus grande précision et d'une façon plus complète, en y ajoutant des démonstrations linéaires et numériques, dans les commentaires que nous t'avons promis précédemment, ô la plus savante et la plus éclairée des femmes, et nous te dirons pour quelles causes nous n'entendons pas nous-mêmes cette symphonie cosmique exhalant des accents suaves et tout harmonieux, comme
la tradition le rapporte (15), Mais, pour le moment, il nous faut continuer sans retard à cause du peu de temps dont nous disposons.
|
(9) Dans l'école de Pythagore. — voir, sur l'harmonie cosmique, Zeller,
Philosophie des Grecs
trad. Boutroux, t. I, p. 407, texte allemand, p. 398. — P.-J. Wallis, Appendix de
Veterum Harmonica ad hodiernam comparata
à la suite de son édition des Harmoniques dee Ptolémée, p. 293, éd. de 1682, excellent travail qui, après deux siècles, n'a presque rien perdu de son utilité.
(10) I1 s'agit ici de l'intensité des sons que les Pythagoriciens mettaient en rapport avec la vitesse vibratoire des tordes et non pas de ce que les modernes appellent la vitesse du son.
(11) Άστήϕ άστατος
(12) Allusion au rapprochement de Αίθήφ et de άείθέων (Cratyle, 410B)
(13) Littéralement la corde la plus élevée. Dans les diagrammes antiques, la note musicale la plus grave occupe le rang le plus élevé
(14) La nète est la note la plus aiguë dans les diagrammes
Mb. 7
(15) Ώςλ όγος ύπογράφει. Meybaum traduit ut ratio subscribit ; mais il s'agit, à notre avis, de la tradition
|
|
CHAPITRE IV
19. Nous disons d'une manière générale que le bruit est une percussion indivise de l'air qui, parvient jusqu'au sens auditif ; que le son est une tension sans largeur (16) de la voix mélodique que la tension est une station et .un :identité; comme grandeur, d'un son sans intervalle.
20. L'intervalle est le chemin parcouru de la gravité à l'acuité et
vice versa ; le système, une réunion de plusieurs intervalles ; si plusieurs coups ou un vent fort vient à frapper l'air environnant et le frappe sur plusieurs points, il en résulte la production d'un son considérable ; celle d'un son faible s'il y a eu peu de coups ou peu de vent ; celle d'un son uni, si les coups ou le vent sont réguliers, d'une force soutenue ; celle d'un son rude, s'ils sont d'une forée inégale ; celle d'un son grave, s'ils frappent
lentement ; celle d'un son aigu, s'ils frappent vivement (17). L'effet produit est nécessairement inverse dans les instruments à vent, tels que flûtes, trompettes, syrinx, hydraules, etc., et d'autre part dans les instruments à cordes, cithare, lyre, spadix, ou leurs analogues. Paraissent être des instruments intermédiaires ou tenant des uns et des autres ou donnant lieu à des effets semblables, les monocordes, appelés vulgairement pandoures et, par les Pythagoriciens,
canons, les trigones parmi les instruments à cordes et les plagiaules (flûtes obliques) ainsi que les photinx, comme le fera voir la suite de notre discours.
21. Dans les instruments à cordes, les tensions plus grandes et plus fortes produisent des sons plus grands et plus aigus, et les tensions plus faibles, des sons plus lents et plus graves. En effet, lorsque le plectrum déplace les cordes, celles-ci, éloignées de leur position propre, tantôt y reviennent en frappant sur beaucoup de points l'air environnant avec une très-grande rapidité et un fort mouvement vibratoire, comme excitées par
l'énergie même e de leur tension; tantôt elles y reviennent posément et sans vibration, à l'instar du cordeau des maçons.
22. Par contre, dans les instruments à vont, les plus grandes cavités et les plus grandes longueurs produisent un son lent et relâché, car le vent s'échappe dans l'air environnant après avoir dépensé, son intensité sur, un long parcours; il le frappe et l'agite d'une façon à peine sensible, et par suite le son produit est grave.
23. Il faut considérer ici que le plus et le moins dépendent de la quantité que nous obtiendrons, soit en surtendant et en relâchant une flûte (18), soit en donnant plus de longueur ou de brièveté aux cordes. Or il est évident que tout cela est réglé numériquement, car on conçoit que la quantité ne peut se rattacher en propre qu'au nombre.
|
(16) Métaphore empruntée à la géométrie qui considère des lignes sans largeur.
Mb. 8
(17) Sur le rapport de la vitesse avec le degré d'intonation, voyez Aristote, Topiques, I, xii, 1, où sont mentionnés χαθ̉ άϕιθμούς άϕμονιχοί
Mb. 9
(18) Les manuscrits connus donnent αύτόυ. Meybaum a corrigé enαύλόυ
|
|
CHAPITRE V
24. Pythagore (19) est le premier qui, pour éviter que, dans la conjonction (20), le son moyen comparé aux deux extrêmes offrît l'unique consonnance de quarte différenciée (21), d'une part avec l'hypate, d'autre part avec la nète, et — pour obtenir que nous puissions envisager une théorie plus variée et que les extrêmes produisant en eux la consonnance la plus satisfaisante, c'est-à-dire celle de diapason (octave) qui
comporte le rapport double (22), ce qui ne pouvait avoir lieu avec les deux tétracordes existants, — intercala un huitième son qu'il agença entre la mèse et la paramèse et qu'il fixa à la distance d'un ton entier de la mèse, à un demi-ton de la paramèse (23). De cette' façon, la corde. qui représentait antérieurement la paramèse dans la lyre heptacorde est appelée encore
trite (troisième) à partir de la nète et occupe néanmoins cette position ; tandis que la corde intercalée se trouve la quatrième à partir de la nète et sonne la quarte avec elle, consonnance que faisait entendre dans le principe la mèse avec l'hypate (24).
25. Le ton placé entre ces deux sons, la mèse et la corde intercalée, qui reçut le nom de l'ancienne paramèse, selon qu'il est adjoint à l'un ou à l'autre des deux tétracordes, tantôt plus nétoïde, adjoint au tétracorde du côté de l'hypate, tantôt plus hypatoïde, adjoint à-celui du côté de la nète, fournira la consonnance de quinte qui constitue des deux côtés
un système formé du tétracorde lui-même et du ton additionnel. C'est ainsi que le rapport sesquialtère (25) de la quinte est reconnu commé la somme du sesquitiers et du sesquioctave (26). Donc le ton est sesquioctave (27).
|
(19) Cp. tout ce chapitre avec un passage correspondant et presque identique de Manuel Bryenne, Harmoniques, liv. I, section I, p. 361-367.
(20) Dans la conjonction des deux tétracordes ayant chacun des sons extrêmes accordés à la quarte et, au milieu, un son 'commun.
(21) Par le degré d'intonation ?
(22) On appelle rapport doubl celui de 2 à 1 ou épitrite celui de 4 à 3, sesquialtère ou hémiole celui de 3 à 2, et sesquioctave (έπόλόος) celui de 9 à 8.
(23) «La théorie musicale des pythagoriciens jusqu'à Philolaüs ne connaît que les sept notes de l'heptacorde.» Zeller, Philosophie des Grecs, trad. Boutroux, t. I, p. 412, texte allemand, p. 402. Et en note : «Il va de soi que l'on ne peut tenir compte ici de l'assertion de Bryenne (Harmoniques, section I, p. 365), qui fait de Pythagore l'inventeur de l'octacorde.»
Mb. 10
(24) Voici un tableau qui résume l'explication de Nicomaque :
|
Nète
|
la
|
|
ton
|
|
|
paranète
|
sol
|
|
ton
|
|
|
trite ou paramèse
|
fa
|
|
demi-ton
|
|
|
Mèse
|
mi
|
|
ton
|
|
|
lichanos
|
ré
|
|
ton
|
|
|
parhypate
|
ut
|
|
demi-ton
|
|
|
Hypate
|
si
|
|
|
|
|
Nète
|
si ou la
|
|
ton
|
|
|
paranète
|
la — sol
|
|
ton
|
|
|
trite
|
sol — fa
|
|
demi-ton
|
|
|
paramèse
|
fa# — mi
|
|
ton
|
|
|
Mèse
|
mi — ré
|
|
ton
|
|
|
lichanos
|
ré — ut
|
|
ton
|
|
|
Parhypate
|
ut — si b
|
|
demi-ton
|
|
|
Hypate
|
si — la
|
(25) Rapport de 3 à 2.
(26) En effet, 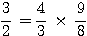
La somme des deux fractions s'obtient par leur multiplication.
(27) En effet, 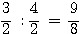
La différence des deux fractions s'obtient en divisant la plus grande par la plus petite. C. Vincent,Notices, etc., p. 297, note.
|
|
CHAPITRE VI
26. Quant à la quantité numérique qui représente la, distance des cordes sonnant la quarte, celle de la quinte, celle qui par leur réunion devient ce qu'on nomme diapason (octave), enfin le ton additionnel placé entre les deux tétracordes, voici comment Pythagore, à ce qu'on affirme, s'y est pris pour s'en rendre compte (28).
27. Un jour qu'il se promenait tout en s'abandonnant aux réflexions et aux pensées que lui suggéraient ses combinaisons, cherchant s'il ne pourrait pas imaginer un secours pour l'oreille, sûr et exempt d'erreur, tel que la vue en possède un dans le compas et dans la règle ou même, disons-le (29), dans la dioptra (30), le toucher dans la balance, ou dans l'invention des mesures, il vint à passer, par une coïncidence providentielle, devant
un atelier de forgeron, et entendit très-distinctement des marteaux de fer (31) frappant sur l'enclume et donnant pêle-mêle des sons parfaitement consonnants entre eux, à l'exception d'un seul couple. Il reconnut, parmi ces sons, les consonnances de diapason (octave), de diapente (quinte) et de diatessaron (quarte). Quant à l'intervalle intermédiaire entre la quarte et la quinte (32), il s'aperçut qu'il était inconsonnant en lui-même ; mais, d'autre
part, complémentaire de la plus grande de ces deux consonnances.
28. Rempli de joie, il entra dans l'atelier comme si un dieu secondait son dessein, et, au moyen d'expériences variées, après avoir reconnu que c'était la différence de poids qui causait la différence de son, et non pas l'effort des forgerons ni la forme des marteaux, ni le déplacement du fer laminé, il releva avec un grand soin le poids des marteaux et leur force impulsive qu'il trouva parfaitement identique, puis il rentra chez lui.
29. Il fixa un clou unique dans l'angle formé par deux murailles, pour éviter qu'il y eût même de ce côté la moindre différence ou que, d'une manière quelconque, la pluralité des clous ayant chacun leur matière propre rendît l'épreuve suspecte. Il suspendit à ce clou quatre cordes semblables par la substance, le nombre des fils ; la grosseur, la torsion, et fit supporter à chacune d'elles un poids
qu'il fixa à son extrémité inférieure. De plus, il rendit les longueurs des cordes de tout point égales, puis frappant ensemble les cordes deux à deux, il réconnut respectivement les consonnances précitées qui variaient avec chaque couple de cordes
30. La corde tendue par la suspension du plus grand poids, comparée avec celle qui supportait le plus petit, lui fit constater une résonnance à l'octave ; or celle-ci représentait 12 des poids donnés, et celle-là 6. Il établit ainsi que l'octave est dans le rapport double, ce que les poids eux-mêmes (33) lui avaient fait entrevoir. La plus grande corde (34), comparée avec celle qui venait après la plus petite et qui représentait
8 poids, sonnait la quinte, et il établit qu'elles étaient dans le rapport sesquitiers, ce qui était aussi le rapport des poids entre eux ; puis il la compara avec celle qui la suivait, par rapport au poids supporté. La plus grande des autres cordes se trouvant avoir 9 poids sonnait la quarte (35), proportionnellement aux poids ; or il constata, qu'elle était dans le rapport inversement sesquitiers (36) et que cette même corde se trouvait par nature sesquialtère
de la plus petite (37), car 9 est à 6 dans le même rapport, de même que la corde proche de la petite et supportant 8 poids était à la corde qui en supporte 6 (38) dans le rapport sesquitiers et à la corde de 12 poids dans le rapport sesquialtère.
34. Par conséquent, l'intervalle compris entre la quinte etla quarte, c'est-à-dire celui dont la quinte surpasse la quarte était confirmé comme se trouvant dans le rapport sesquioctave qui est celui de 9 à 8. Le diapason (octave) était le système formé par la réunion de l'une et de l'autre, autrement dit de la quinte et de la quarte placées en conjonction (39) ; de même que le rapport double se compose du sesquialtère
et du sesquitiers, soit 12, 8, 6 (40) ; ou inversement, par la réunion de la quarte et de la quinte, de même que le double se compose du sesquitiers et du sesquialtère, soit 12, 9, 6, placés dans cet ordre.
32. Après avoir exercé sa main et son oreille à l'étude des poids suspendus et bien établi d'après ces poids le rapport des proportions constatées (41), il transporta ingénieusement les résultats généraux obtenus par les cordes, (lesquels provenaient du clou placé dans l'angle des deux murailles), sur la
batère (la tablette inférieure) (42) d'un instrument qu'i1 nomma
cordotone, et la tension, portée à un point proportionnel à celles que produisaient les poids, passa dans le mouvement des chevilles placées à la partie supérieure. Une fois installé sur ce terrain et comme qui dirait en possession de ce gnomon infaillible, il étendit l'expérience en la faisant sur divers instruments, par exemple au moyen de la percussion des vases (42), sur les flûtes, les syrinx; les monocordes, les trigones et autres
semblables ; toujours il trouva consonnante. et invariablement sûre la détermination indiquée par les nombres (43).
33. Il nomma
hypate le son correspondant au nombre 6,
mèse, le son 8, qui se trouve être son sesquitiers ;
paramèse, le son 9, plus aigu d'un ton que le son moyen (44) et par conséquent son sesquioctave ; enfin
nète, le son 12. Ensuite il suppléa les points intermédiaires, suivant le genre diatonique, au moyen de sons proportionnels et subordonna ainsi la (lyre) octacorde aux nombres (45) consonnants, savoir le double, le sesquialtère, le sesquitiers, et à la différence de ces deux derniers, le sesquioctave.
|
(28) L'expérience qui va suivre a été décrite, depuis Nicomaque par Gaudence (p. 13, de Meybaum), Jamblique (Vie de Pythagore, I, xxvii), Boèce (De Musica, x), Macrobe (Somn. Scip., 1. II, ch. 1) et l'Hagiopolite publié par Vincent (Notices, p. 266). Le savant académicien a donné à ce propos un commentaire étendu de la description rapportée par notre auteur. Cp. Zeller (Philosophie des Grecs, trad.
Boutroux, t. I, p, 385, texte allemand, p. 370), qui voit «un conte» dans le récit de l'expérience des rmarteaux. Voir aussi Th.. Henri Martin, Études sur le timée, t. I, p. 38'9 et suiv.
(29) Nή Δί
(30) Héron d'Alexandrie; a écrit un traité de la Dioptra publié et, traduit pour la première fois par A.-J.-H. Vincent (Notices et extr. des mss., etc., t. XIX, 2e partie).
Mb. 11
(31) Voir Vincent,
Notices, etc., p. 274, qui propose de remplacer les marteaux (Σϕϋραι) par des globes creux σϕαϊραι, alléguant qu'un texte publié par lui (V• fragment de l'Hagiopolite, p. 266) donne cette leçon.
(32) Ou plutôt l'intervalle qui fait la différence entre la quarte et la quinte.
Mb. 12
(33)Les poids des marteaux résonnant sur l'enclume.
(34) Toutes les cordes sont d'égale longueur, mais l'auteur appelle elliptiquement la plus grande celle qui supporte le plus grand poids.
(35) Toujours avec la plus grande corde.
(36) En effet, 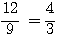
(37) En effet, 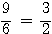
(38) En effet, 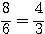
(39) Se succédant sans interruption.
Mb. 13
(40) 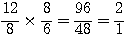 ; et ; et
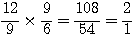
(Cp. ch. 26, notes)
(41) Les rapports réels des sons ne sont pas ceux des tensions des cordes ou des poids des marteaux, mais ceux des racines carrées des forces de tension.βατήρ de la lyre, tablette d'où partaient les cordes tendues au moyen de chevilles à la partie supérieure.
(42) Ces mots infirment la correction (σϕϋραι) proposée par M. Vincent.
(43) Aristide Quintilien rapporte que Pythagore, en mourant, fit à ses disciples la recommandation d'étudier le monocorde, μονοχορόίζειν. (De Musica, 1. III, p. 116.)
(44) La mèse.
(45) Ici et ailleurs, le mot nombre est pris dans le Sens de rapport.
|
|
CHAPITRE VII
34. Pythagore reconnut de la manière suivante, en vertu d'une nécessité naturelle, la progression des sons depuis le plus grave jusqu'au plus aigu, suivant ce même genre diatonique; car, pour le chromatique et l'enharmonique, il les décrivit plus tard d'après celui-ci, comme nous aurons à l'exposer un jour. Donc ce genre diatonique parait avoir, par nature, certains degrés et certains procédés dont voici le détail.
Un demi-ton, un ton, un ton, ce qui forme un système de quarte, composé de deux tons et de ce qu'on appelle demi-ton (46) ; puis, par l'addition d'un. autre, ton, c'est-à-dire le ton intercalé, i1 en résulte le système de quinte composé de trois tons et d'un demi-ton.. Viennent ensuite un demi-ton, un. ton, un ton, autre système de quarte, c'est-à-dire sesquitiers.
35. Ainsi donc, dans la lyre heptacorde, antérieure à celle-ci, tous les quatrièmes sons à partir du plus grave consonnaient toujours entre eux à la quarte, le demi-ton occupant tour à tour, par suite de son déplacement, le premier degré, le degré moyen et le troisième du tétracorde (47) ; tandis que dans la. lyre pythagoricienne, dite octacorde, tantôt; — dans le cas de la conjonction, — il y a un système
composé d'un tétracorde et d'un pentacorde, tantôt, — dans le cas de la disjonction, — deux tétracordes étant séparés l'un de l'autre par l'intervalle d'un ton, la progression aura lieu, à partir de la corde la plus grave, de telle façon 'que tous les cinquièmes sons consonnent entre eux à la quinte, le demi-ton occupant tour à tour quatre degrés différents, le premier, le second, le troisième et le quatrième
(48).
|
(46) On voit que ce terme répugne au pythagoricien Nicomaque. On disait, dans cette école, un limma. Comment le savant Montucla peut-il écrire, dans sonHistoire des mathématiques
(t. I, p. 313), que Nicomaque est Aristoxénien dans son Manuel ! Notre auteur n'est Aristoxénien que sur les points où les deux écoles sont d'accord.
(47) It faut comprendre le premier degré, le troisième et le moyen. Le mot tétracorde est pris ici dans le sens de « série de quatre sons .renfermée dans les limites de la quarte n'et non dans le sens commun de « tétracorde limité par des sons fixes ».
(48). Il.faut comprendre : le premier, le quatrième, le troisième et le second., — Cp. Aristoxéne
harm., p. 59, éd. Mb.
|
|
CHAPITRE VIII
36. Arrivés à ce. point, c'est le moment pour nous de commenter le passage de la
Psychogonie (49) où Platon s'exprime en ces termes.
C'est pourquoi, dans chaque intervalle, il y a deux moyennes, l'une est supérieure et inférieure aux extrêmes d'une même fraction (50), l'autre, supérieure d'une d'une quantité numérique égale et inférieure d'une quantité.égale aussi (51) à chaque extrême respectivement. Il (le démiurge) remplit la distance qui sépare les intervalles sesquialtères et sesquitiers avec l'intervalle (52) du sesquioctave.
»
37. En effet, l'intervalle double (53), c'est le rapport de 12 à 6, et les deux moyens, ce sont le nombre 9 et le nombre 8 ; mais le nombre 8, dans la proportion harmonique, est moyen entre 6 et 12, étant supérieur à 6 du tiers de ce nombre 6 et inférieur à 12 du tiers de ce nombre 12. Voilà pourquoi (Platon) dit que c'est de la même fraction, considérée dans les extrêmes eux-mêmes, que la moyenne 8 est respectivement supérieure
et inférieure ; car ce que le plus grand terme est au plus petit, savoir le double, la différence du plus grand d'avec la moyenne, différence qui est 4, l'est à la différence de cette moyenne d'avec le plus petit, différence qui est 2 ; et, en effet, ces (différences) sont en rapport double comme 4 est à 2.
38. Le caractère propre de cette moyenne, c'est que la somme des extrêmes multipliée par la moyenne donne un produit double du produit des extrêmes (54). En effet, 8 fois la somme des extrêmes qui est 18 font 144, double du produit des extrêmes, qui est 72.
39. L'autre moyenne, 9, placée au rang de la paramèse, est considérée comme moyenne arithmétique entre les,extrêmes, étant, de 3 unités, inférieure à 12 et supérieure à 6. Son caractère propre, c'est que la somme des extrêmes est le double de cette moyenne, et que le carré de la moyenne, qui est 81 est supérieur au produit des extrêmes d'une quantité égale au carré juste des
différences, c'est-à-dire de 9, carré de 3, car ce dernier nombre est la différence (55).
40. On peut encore faire voir la troisième proportion 7qui est la proportion proprement dite, dans les deux termes moyens 9 et 8 ; car 12 est à 8 comme 9 est à 6 ; ces deux rapports sont sesquialtères, et le produit des extrêmes est égal au produit des moyens. 6 fois 12 égalent 9 fois 8 (56).
|
(49) Autrement dit,le chapitre du Timée où Platon expose la génération de l'âme, p. 36 A.Cp. Th.-Henri Martin,Études sur le Timée, note xxiii
(50) Exemple : Dans la proportion musicale, 12 : 8 :: 8 : 6, le moyen 8 est surpassé par 12 et 9 surpasse 6 de la même fraction, c'est-à-dire du tiers de chaque extrême. C'est la proportion harmonique.
(51) Exemple : 12 : 9 :: 9 : 6. 9 est supérieur à 6 et inférieur à 12 d'une quantité numérique égale, savoir : le nombre 3. C'est la proportion arithmétique.
52) Vulgate, λείμματι. Fort. legend. διαλείμματι. Cicéron, qui a traduit ce passage de Platon (Timæus,
§ 30), donne sesquioctavo intervallo. Platon lui-même emploie ici le mot διάστηα (Timée, 36 A.)
(53) Intervalle correspondant au rapport double ou de 2 à 1.
(54) Exemple : soit la proportion harmonique : 12 : 8 :: 8 : 6 ; (12 + 6) X 8 = 12 X 6 X 2
(55) 3 = 12 - 9 et 9 - 6 ; or (9² = 81) = (12 X 6) + (3² = 9).
(56) La proportion géométrique.
(57) Rapprocher de ce chapitre Théon de Smyrne, ouvr. cité, p. 133 éd. Bouilliau ; p. 85, éd. Hiller (coll. Teubner).
|
|
CHAPITRE IX
41. Que dans une haute antiquité l'on ait avancé des assertions en accord avec ce que nous venons d'exposer, appelant
harmonie le diapason (octave) et
syllabe le diatessaron (quarte), car c'est le premier groupe (σύλλμψις) de sons consonnants (58), et
dioxie le diapente (quinte), car la quinte est la consonnance qui fait immédiatement suite à la consonnance primitive, la quarte, en procédant vers l'aigu ; et que le système formé par l'une et l'autre (la syllabe et la dioxie) soit l'octave ; enfin, qu'on l'ait nommée
harmonie parce que c'est la première consonnance composée de consonnances, voilà ce que Philolaüs, successeur de Pythagore, a mis en lumière dans les termes qui suivent, au livre Ier de sa
Physique ; car nous nous bornerons à un seul témoignage pour aller plus vite, bien que beaucoup d'autres aient donné là-dessus un grand nombre d'explications analogues.
42. Voici comment s'exprime Philolaüs :
La grandeur de l'harmonie comprend une syllabe et une dioxie. La dioxie surpasse la syllabe d'un sesquialtère, car il y a de l'hypate à la mèse une syllabe, de la mèse à la nète une dioxie, de la nète à la trite (59) une syllabe, et de la trite à l'hypate une dioxie. L'intervalle compris entre la trite et la mèse est sesquioctave. La syllabe comprend un intervalle sesquitiers, celui de la dioxie est sesquialtère et celui de l'octave
est double. Ainsi l'harmonie comprend cinq sesquioctaves et deux diésis (60) ; la dioxie, trois sesquioctaves « et un diésis ; la syllabe, deux sesquioctaves et un «diésis.»
43. I1 faut se rappeler que, dans ce passage, (Philolaüs) nomme trite ce qui était paramèse dans la lyre heptacorde avant l'intercalation du ton disjonctif qui eut lieu dans la lyre octacorde ; car cette corde était éloignée de la paranète d'un trihémiton incomposé (61). Sur cet intervalle, la corde intercalée préleva un ton, et le demi-ton restant entre la trite et la paramèse fut absorbé dans la disjonction (62). Par suite,
l'ancienne trite était régulièrement éloignée de la nète de l'intervalle d'une quarte, intervalle que là paramèse a déterminé à la place de cette trite
44. Il y a des gens qui, ne comprenant pas cela, le contestent, alléguant qu'il n'est pas possible que la trite soit éloignée de la nète d'un intervalle en rapport sesquitiers. D'autres émettent cette opinion, qui n'est pas improbable, que le son intercalé n'a pas été placé entre la mèse et la trite, mais entre la trite et la paranète, et que c'est à lui qu'on a donné le nom de trite repris à celle-là (paramèse)
; puis, que, à son tour, la trite est devenue paramèse dans la disjonction ; mais que Philolaüs a donné à la paramèse l'ancienne appellation de trite, bien qu'elle fût éloignée de la nète de l'intervalle de quarte.
|
(58) Autre expression elliptique pour dire groupe de sons dont les deux extrêmes sont consonnants.
Mb. 17
(59) Philolaüs parle de l'ancienne trite de la lyre heptacorde, devenue la paramèse depuis la réforme de Pythagore.
(60) Deux demi-tons.
(61) C'est-à-dire ne comportant pas d'autres sons mélodiques dans son étendue. Vulgate, ήμιτόνιον. Correction de Meybaum
(62) Le mot disjonction, pris absolument,, signifie l'éloignement, de l'interralle d'un ton, des deux tétracordes qui, antérieurement, se faisaient immédiatement suite. — Cette dernière phrase ne peut s'expliquer que par l'existence d'un heptacorde ainsi composé (fig. 1) transformé en octacorde (fig. 2) :
|
Fig. 1
Heptacorde
Nète
Paranète
Trite-paramèse
Mèse
Lichanos-hypermèse
Parhypate
Hypate
|
Fig. 2
Octacorde
Nète
Paranète
Trite
Paramèse
Mèse
Lichanos
Parhypate
Hypate
|
On ren rquera que l'heptacorde, ici, a les sons extrêmes accordés à l'octave. Cp. Aristote, Problémes musicaux, § 32 ; Ptolémée, Harmoniques, 1. II, ch. iv ; fragment de l'Hagiopolite, éd. Vincent (Notices,p. 261 ; voir aussi mon article, Revue et gaz. musicale, 1818, p. 172).
|
|
CHAPITRE X
45. Maintenant revenons sur nos pas en rattachant à l'explication donnée précédemment celle qui va suivre, et en disant que c'est dans le sens inverse de la corrélation en fait de tension qui rend les sons aigus quand il y a multiplicité [de vibrations] et les rend graves quand il y a petit nombre, que l'on vient à établir une théorie sur la longueur ou la grosseur des cordes et sur les dimensions des trous des flûtes, observant
à d'autres égards une proportion inverse de cette théorie (63). En effet, parmi les premières (les cordes), les plus courtes donnent des sons aigus et les plus longues des sons graves.
46. Si, par exemple, prenant une corde longue placée, sur un canon (règle), soumise à une tension constante, mais élevée au-dessus de ce canon de façon qu'elle n'y touche pas, on compare le son produit par le toucher de la corde entière avec le son de sa moitié, considérée isolément au moyen d'un curseur ou de tout autre appareil placé en son milieu, afin que la vibration obtenue par le toucher n'affecte rien que la moitié
considérée, on trouvera l'intervalle de diapason (octave) entre le son de la demi-corde et celui de la corde entière, en rapport plus grand, c'est-à-dire double, l'effet produit étant en raison inverse des données réciproques de longueur.
47. Si, après avoir mesuré exactement un tiers de la corde, on obtient la vibration, le son produit par les deux autres tiers sera nécessairement en rapport sesquialtère avec le son de la corde entière, en raison inverse de la longueur.
48. Si l'on ne frappe que le quart de la corde dans la résonnance qu'on lui fait rendre, sans laisser aller plus loin la vibration, le son des trois quarts de la corde, comparé à celui de sa totalité, donnera un sesquitiers, toujours inversement du rapport de la longueur (64).
49. Il en est de même d'une flûte dont les trous, au nombre de trois, la divisent en quatre longueurs égales et dont les premiers trous (65) sont bouchés au moyen de l'application des doigts. Si nous comparions le son donné par la flûte entière avec celui que rendrait le trou du milieu, quand on suspend l'application du doigt, on trouverait le rapport double, et l'intervalle du son donné par le trou du milieu au son de la flûte entière serait reconnu
pour être l'octave.
50. Le même son (du milieu) comparé au son donné par le son placé au-dessous de lui et auprès du bout inférieur (βατήρ), donnerait le rapport sesquialtère et ce dernier son, comparé au son de la flûte entière, le rapport sesquitiers.
51. Le son donné par le trou placé du côté de la bouche (66), comparé au son donné par le trou du milieu, donnerait le rapport double, et comparé avec le son de la flûte entière, le rapport quadruple (67), toujours en raison inverse des longueurs.
52. En ce qui concerne les syrinx, les longueurs produisent un effet semblable, ainsi que la largeur des tuyaux. De môme encore la grosseur des cordes; car les cordes à deux fils rendent un son double (4) de celui des cordes à quatre fils.
|
(63) Cp. ci-dessus, ch. iv, § 20.
Mb. 19
(64) Un habile acousticien de Messine, M. Arc. Camiólo, a inventé et fait exécuter un appareil sur lequel il serait facile d'expérimenter toutes les questions de musique mathématique agitées par les Pythagoriciens.
(65) Les premiers trous à partir des deux bouts de la flûte. Peut-être faut-il lire άχρων au lieu de πρώτων et supposer que les manuscrits ont donné successivement : άχρων, lu άων, d'où πρώτων, ce qui n'a rien d'invraisemblable.
(66) Littéralement, du côté de la langue.
(67) Rapport correspondant à l'intervalle de disdiapason ou double octave.
Mb. 20
(68) C'est-à-dire à l'octave aiguë.
|
|
CHAPITRE X
53. Voici en quoi consiste le corps du diagramme dans le genre diatonique.
Il comprend la double octave et sa largeur est quadruple (69) ; car c'est tout ce que peut faire la voix de concours (70) sans danger et sans encombre, étant exposée, lorsqu'elle excède ces limites, à tomber dans la voix de fausset, si elle avance plus loin vers la nétoïde (71) et dans le bruit de la toux si elle se risque jusqu'à un degré de bourdon plus grave.
54. A la lyre antique, c'est-à-dire heptacorde, composée de deux tétracordes reliés en conjonction et tels que la mèse en faisait deux intervalles consonnants, l'un, le plus grave, du côté de l'hypate, se dirigeant vers l'aigu (72), et l'autre, du côté de la nète, se dirigeant vers le grave, on adjoignit deux autres tétracordes, un à chaque extrémité.
55. Du côté de la nète primitive, il y eut le tétracorde dit des
hyperboléennes (73), parce qu'il était établi sur un degré vocal plus aigu et transcendant (ύπερϐάλλων), commençant avec l'ancienne néte et placé en conjonction, de telle façon que la surtension de ce tétracorde fut limitée à l'adjonction de trois (nouveaux) sons seulement qui reçurent à bon droit les dénominations suivantes :
Trite des hyperboléennes, [
paranète et] (74) nète des mêmes.
56: Afin d'établir une distinction et d'éviter (75) que le tétracorde, placé avant celui-ci et relié en conjonction avec la mèse, eût ses sons dénommés de la même manière, le son placé après la mèse fut appelé
trite des conjointes ; vient ensuite la
paranète des conjointes, et l'ensemble nétoide partant de la mèse redevient encore lui aussi un heptacorde (76).
57. Du côté de l'hypate primitive, dans le sens du grave, on adjoignit, toujours par conjonction, l'autre tétracorde en question, dans lequel se fit entendre aussi l'ancienne hypate comme son le plus aigu de ceux qu'il renfermait. De la même façon (que tout à l'heure), pour marquer une distinction avec la disposition du tétracorde précédent, le nouveau reçut aussi des noms plus significatifs et à chaque nom de son fut ajouté le
terme : des hypates (ύπατων) (77) ; exemples :
hypate des hypates,
diatonique des hypates ou
lichanos des hypates, car on dit les deux indifféremment (78).
58. Le système total compris entre la mèse et l'hypate des hypates se trouvait former un heptacorde composé de deux tétracordes conjoints et (79) employant un son commun, l'ancienne hypate. On eut donc ainsis depuis l'hypate des hypates jusqu'à la nète des hyperboléennes, quatre tétracordes conjoints [deux à deux], et le tout se trouvait former une somme de treize cordes, dont la septième, à partir de chaque extrérnité,
était fixée à un.ton de distance (80), puisque, comme on l'a dit plus.haut (81), le huitième son fut intercalé à la distance d'un ton entre la mèse et l'ancienne trite par ceux qui voulurent jeter de la variété dans l'harmonie, ou, suivant quelqnes uns, entre la.trite et la paranète, ce qui amena l'apparition de la quinte. La corde nommée,
mèse, (moyenne) ne fut plus une mèse, car dans un agencement de cordes en nombre pair il ne peut y avoir une corde moyenne, mais il y a nécessairement une septième et une huitième. On ajouta donc, par-delà l'hypate, un son extrême, le plus grave des sons existants, qui en raison de son origine reçut le nom de son
proslambanomène (additionnel), placé un ton au grave de l'hypate des hypates, de telle façon que les systèmes placés de chaque côté de la mèse furent octacordes et que la mèse devint réellement. une mèse (corde moyenne) entre quinze sons, étant la huitième corde à partir de chaque (extrémité de l'échelle). Il résulta aussi de là que la double octave .formant l'étendue
totale du diagramme devint doublement double, c'est-à-dire quadruple, et que l'ordre des dénominations fut celui-ci (81) :
Le proslambanomène;
Puis, à la distance d'un ton juste,
l'hypate des hypates ;
Un demi-ton après,
la parhypate des hypates;
Un ton après, la
lichanos des hypates ; ce nom (de lichanos) lui vient de ce que le doigt de la main gaüche, voisin du pouce, appelé de ce même nom de lichanos (index), est toujours appliqué sur cette corde;
Puis, un autre ton après,
l'hypate des moyennes ;
Un demi-ton à.la suite, la.
parhypate des moyennes ;
Un ton après, la
lichanos des moyennes, qui s'appelle aussi diatonos, empruntant ce nom au genre diatonique lui-même. (82).
Ensuite un autre ton aprè, la
mèse ;
Puis la
paramèse, un ton juste après ;
La
Trite des disjiontes, un demi-ton après ;
Puis, un ton après, la
paranète des disjointes ;
Un autre encore après,
la nète des disjointes ;
Un demi-ton à la suite, la
trite des hyperboléennes ;
Un ton après, la
paranète des hyperboléennes ;
Et enfin, un ton après,
la nète des hyperboléennes.
59. De plus, en mémoire de la conjonction qui avait lieu primitivement dans l'heptacorde, on intercala, entre le tétracorde des moyennes et celui des disjointes, un autre tétracorde dit
conjoint, dont la trite se place après la mèse, à la distance d'un demi-ton ; puis, un ton après vient sa paranète propre ; puis, un. autre ton après, la nète conjointe (83), qui a exactement la même tension et le même son que la paranète disjointe (85).
60. Ainsi donc les tétracordes sont en tout au nombre de cinq, savoir ceux des
hypates, des
moyennes, des
conjointes, des
disjointes et des
hyperboléennes ; leurs disjonctions au nombre de deux, et leurs conjonctions au nombre de trois. Les disjonctions ont lieu, l'une entre le tétracorde des moyennes et celui des disjointes (86), l'autre entre le proslambanomène et l'hypate des hypates.Chacune, d'elles comprend la distance d'un ton. Les trois conjonctions ont lieu, la première entre,le tétracorde des hypates et celui des moyennes, la seconde.entre celui des moyennes et celui des conjointes, la dernière
entre celui des disjointes et celui des hyperboléennes.
61. Pour ce qui concerne la découverte de tous ces éléments, son par son, leurs causes, leurs procédés, leur mode de production, leurs inventeurs, l'époque et les circonstances de leur invention, nous en ferons l'exposé tout au long un jour, en commençant par le tétracorde pour finir par la catapycnose la plus complète du diapason (octave) (87), non-seulement dans le genre diatonique, mais encore dans le chromatique et dans l'enharmonique,
en citant le témoignage des anciens les plus autorisés et les plus savants. Puis nous décrirons la division de ce qu'on nomme le canon de Pythagore, exécutée d'une façon rigoureusement conforme à l'intention de ce maître, non pas suivant la fausse interprétation d'Ératosthène ou de Thrasylle (88), mais comme l'entendait Timée de Locres, que Platon a suivi jusqu'au vingt-septuple (89).
|
(69) En d'autres termes, son étendue correspond au rapport quadruple, de 4 à 1, qui est celui de la double octave:
(70) Έναγώνις. Traduction conjecturale.
(71)- Le (degré) nétoÏde, la (région) nétoïde correspond plus ou moins à la voix de mezzo-soprano pour les femmes : Voir Vincent, Notices, etc., p. 20, 31 et 120
(72) pour gagner cette mèse.
(73) Tétracordes des adjointes dans la terminologie de M. Vintent (Notices, p. 119.)
(74) Lacune dans les manuscrits connus.
(75) On propose ϊνα μή
au lieu de ϊνα όή
.
Mb. 21
(76) Ou plutôt le tétracorde partant de la mèse et allant vers le grave forme avec celui qui partait de cette corde à l'aigu un système conjoint heptacorde ; car il n'y a pas de système heptacorde ayant la mèse comme limite grave.
<
(77) Des fondamentales dans la terminologie de Vincent.
(78) L'auteur aurait pu ajouter : dans le diatonique exclusivement, mais il est convenu que nous sommes actuellement dans ce genre.
(79) Lu χαί
au lieu de χαν
(80) Exemple unique, sauf erreur du mot δίατονεχό
exprimant l'étendue d'un ton. Aristoxène emploie le mot τονεαϊος.
(81) Ci-dessus, § 43.
(81) Georges Pachymère a reproduit` cet Morceau jusqu'à la fin, de notre § 60. (Vincent, Notices, etc., p..449.
(82) Comme c'est la seule note qui change autant de fois de position, dans le tétracorde, qu'il y a de variétés de genre, elle devient ainsi la caractéristique de ces variétés et peut prendre par suite le nom du genre auquel elle appartient. Elle s'appelle diatonos dans le genre diatonique, chromatique dans le chromatique, enharmonios dansl'enhartmonique. Voir ma traduction d'Aristoxène, Él. harm., plache 2. M. Vincent a nommé
cette corde l'indicatrice. (Notices, etc., p. 119) Cp. Ariside Quintilien, p. 10.
Mb. 23
(83) Nommée plus communément nète des conjointes.
(84) Dans le génie diatonique, le seul en question ici.
(85) Dans le genre diatonique, le seul en question icic
(86) Le texte est altéré, mais le sens ne fait pas de doute
(87) Καταπύχγωσις,
morcellement ; subdivision d'un systéme décomposé en intervalles minimes, c'est-à-dire en quarts de ton. Aristoxène critique la catapycnose. Voir ma traduction de ses Él. harm. 1. 1, chap. ii, § 21, p. 7 de l'éd. Meybaum. — Cp., p. 38, même édition.
Mb. 24
(88) Sur Eratosthène, voir Bernhardy, Eratosthenica, 1822, p. 170 et suiv. - Thrasylle est cité par Suétone, Aug. et Tib., et par le scholiaste de Juvénal , in Sat. VI, vers 576, comme un mathématicien, ami de Tibère. Cp. Théon de Smyrne, ouvr. cité, p. 74, 133 et surtout 137, éd. Boulliau ; Ptolémée, Harmonique, II, xiv, tableaux 2 et 3.
(89) Cp. Platon, Timée, p. 35 C. Voir plus loin le prétendu livre II de Nicomaque, 2e fragment
|
|
CHAPITRE XII
62. Pour que tu possèdes la progression particulière à chacun des trois genres et le développement régulier (des sons) depuis le proslambanomène jusqu'à la nète des hyperboléennes, il convient que je reprenne mon exposé un peu plus haut, en touchant d'abord, pour plus de clarté les points dont j'ai déjà parlé.
63. Le son est une émission de voix indivisible, comme l'unité, par analogie, ou, comme disent le smocernes (90) la chute de la voix sur une tension simple et unique, ou encore, selon quelques-uns, un bruit sans largeur et sans intervalle quant au lieu.
64. L'intervalle c'est le milieu existant entre deux sons
65. Le rapport, c'est la proportion qui sert à mesurer la ddistance dans chaque intervalle.
66. La différence, cest l'excès ou le défaut parmi les sons comparés entre eux ; car c'est mal juger que de croire que la différence et le rapport sont la même chose. Prenons un exemple. De 2 à 1, il y a la même différence que de 1 à 2 mais non pas le même rapport, car 2 est le double de 1, tandis que 1 est la moitié [de2] (91). De plus, parmi tous les termes d'une proportion arithmétique, qu'il y en ait trois ou plus, la
différence est la même entre tous, tandis que le rapport varie de l'un à l'autre. Du reste, tu trouveras là-dessus de plus amples informations dans mon grand commentaire.
67. Le système est la réunion de deux ou de plus de deux intervalles en un seul. Dans les intervalles, un son n'est jamais consonnant avec celui qui le suit immédiatement, il est toujours dissonant : tandis que parmi. les systèmes quelques-uns sont consonnants et d'autres dissonants.
68. Les systèmes sont consonnants lorsque les sons qui, les comprennent, différents de grandeur, touchés ensemble (92) ou d'une façon quelconque se mélangent de telle façon entre eux qu'il en résulte la production d'une émission vocale uniforme et en quelqné sorte unique.
69. Deux sons au contrairè sont dissonants lorsque l'émission vocale qui en résulte arrive à l'oreille démembrée jusqu'à un certain point et non mélangée.
70. Maintenant, comme le premier consonnant et le plus élémentaire est la quarte, dans un tétracorde continu (93), suivant un rapport sesquitiers, il est rationnel de trouver dans ce (système) les variations des trois genres de la mélodie.
71. Le diatonique, dont nous avons parlé plus haut, procède ainsi (94) : un demi-ton ; un ton, puis un ton, en tout trois intervalles compris entre quatre nombres, c'est-à-dire quatre sons. Ce nom de diatonique lui vient de ce que c'est absolument le seul qui procède par tons.
72. Le chromatique procède ainsi un demi-ton, un demi-ton, puis enfin un trihémiton incomposé, de façon qu'il arrive ceci que , bien qu'il ne se compose pas manifestement de deux tons et d'un demi-ton, on y retrouve néanmoins une somme d'intervalles égale à deux tons et demi.
73. L'enharmonique a, par nature, la progression.que voici : un diésis, ce qui est la moitié d'un demi-ton, puis encore un autre diésis, ce qui fait en tout un demi-ton, et le reste du tétracorde, un diton juste incomposé, de telle façon que ce système, lui aussi, est égal à deux tons et demi ; car, entre ces divers intervalles, il est impossible qu'un son consonne avec un autre son.
74. Il est donc évident que les variations de genres ne tirent pas leurs différences des quatre sons qui composent la quarte, mais seulement des deux sons moyens (du tétracorde).
75. Dans le chromatique, c'est le troisième son qui varie par rapport au diatonique, tandis que le deuxième reste le même et a la même tension que le troisième son de l'enharmonique.
76. Dans l'enharmonique, les deux moyens varient par rapport au diatonique, de sorte que l'enharmonique est l'opposé du diatonique, et que le chromatique est entre les deux ; car il s'éloigne de peu, d'un demi-ton seulement, du diatonique. De là cette expression : « être nuancé », que l'on applique à. l'homme versatile (95).
77. Les sons extrêmes d'un tétracorde se nomment
sons fixes, car ils ne se déplacent dans aucun genre, et les
sons moyens, sons mobiles, du moins dans l'enharmonique, tandis que, dans le chroma, le second est à la fois mobile et non mobile, car par rapport au diatonique il ne se déplace pas, et, par rapport à l'enharmonique, il se déplace.
78. L'octave, qui est un système allant soit de la mèse au proslambanomène, soit de la mèse à la nète hyperboléenne, et qui se compose de huit cordes, la consonnance de quarte se composant de deux tons plus un demi-ton, et celle de quinte de trois tons plus un demi-ton, ne comprend pas exactement six tons comme le croient les modernes (96), mais cinq tons et deux intervalles appelés demi-tons. Si c'étaient là réellement des demi-tons,
qu'est-ce qui empêchait qu'un ton résultât de leur somme, et que la consonnanee se composât de six tons ? Au surplus, nous exposerons clairement et dans tous les détails la démonstration de ce fait au cours de notre grand commentaire, et Philolaüs nous prêtera son autorité par la citation donnée plus haut, en disant : «L'harmonie contient cinq sesquioctaves et deuxdiésis», c'est-à-dire deux demi-tons qui font un ton, puisque
(ces diésis) étaient en réalité des moitiés de ton.
79. Maintenant, si nous entremêlons dans le même diagramme les sons des trois genres, nous aurons la nomenclature suivante :
Proslambanomène;
Hypate des hypates ;
Parhypate des hypates enharmonique ;
Parhypate des hypates chromatique et diatonique ;
Enharmonique des hypates ;
Chromatique des hypates ;
Diatonos des hypates ;
Hypate des moyennes ;
Parhypate des moyennes enharmonique ;
Parhypate des moyennes chromatique et diatonique ;
Enharmonique des moyennes; Chromatique des moyennes ; Diatonos des moyennes ;
Mèse ;
Trite des conjointes enharmonique ;
Trite des conjointes chromatique et diatonique ;
Enharmonique des conjointes ;
Chromatique des conjointes ;
Diatonos des conjointes ;
Nète des conjointes ;
Paramèse ;
Trite des disjointes enharmonique ;
Trite des disjointes chromatique et diatonique ;
Enharmonique des disjointes ;
Chromatique des disjointes ;
Diatonos des disjointes ;
Nète des disjointes ;
Trite des Hyperboléennes enharmonique ;
Trite des hyperboléennes chromatique et diatonique ;
Enharmonique des hyperboléennes ;
Chromatique des hyperboléennes ;
Diatonos des hyperboléennes ;
Nète des hyperboléennes
80. Tu excuseras la précipitation avec laquelle j'ai rédigé cet écrit, car tu sais bien que tu me l'as demandé pendant que j'étais en voyage et que j'ai dû le faire au pied levé. Puisse ton esprit, si indulgent, si judicieux, l'agréer comme des prémices et un hommage destiné à me concilier ta faveur, en attendant qu'avec la permission des dieux je t'adresse, incessamment, par la première occasion, un traité complet
et définitif sur ces matières !
|
(90) Nicomaque.appelle ainsi les Aristoxéniens. Cp. Aristoxène, Él. harm, p. 17 de ma traduction, p. 13 éd. Meybaum..
Mb. 25
(91) Cp. Théon de Smyrne, ouvr. cité, p. 127, éd..Boulliau.
(92) Comme dans l'harmonie moderne.
(93) Pour que la quarté, considérée sur deux tétracordes, comprenne quatre sons mélodiques, il faut que ces tétracordes soient conjoints, continus. Cp. Aristoxène, El. harm., 1. III, ch.i, p. 59 de Meybaum.
(94) Les énumérations, ici, vont toujours du grave à l'aigu. Chez Platon c'est le contraire. Cp. Martin, Études sur le Timée; I, p. 401.
Mb. 26
(95) Chromatique veut dire Coloré, nuancé. Nous disons encore aujourd'hui d'un homme qui change souvent d'avis : C'est un caméléon.
Mb. 27
(96) L'auteur vise les.Aristoxéniens.
Mb. 28
|
À propos S'abonner au bulletin Liste musicologie.org Collaborations
éditoriales 

Références / musicologie.org 2012
|





|
![]()

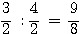
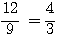
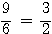
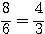
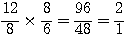 ; et
; et